|
|
||||
|---|---|---|---|---|
Inhalt:
|
||||
|
Ordnung und Chaos... ...liegen in der Natur näher beieinander als man denkt. Das zeigt sich an dem einfachen Röhren-Oszillator rechts im Bild. Statt der einfachen Sinusschwingung erzeugt er nach einer Reihe von Periodenvervielfachung immer komplexere Schwingungsformen. Und schließlich wird die Schwingung chaotisch und völlig unvorhersagbar. Die Schaltung zeigt einen einfachen Tongenerator, der nach dem Meißner-Prinzip funktioniert. Wesentliche Bestandteile sind eine Verstärkerpentode vom Typ EF89 und der Transformator beziehungsweise Tonfrequenzübertrager. Seine beiden Wicklungen haben ein Übersetzungsverhältnis von etwa 1 zu 2,4. Die Induktivität L1 der Wicklung im Gitterstromkreis ist gemeinsam mit den beiden in Serie geschalteten Kondensatoren C1 und C2 für die Frequenz verantwortlich. Außerdem bilden sie einen Spannungsteiler, der die recht hohe Amplitude der Wechselspannung an L1, bis zu 100 Volt, auf 10 Volt für das Röhrengitter heruntersetzt. Die Schaltung ist auch mit anderen gängigen Radiopentoden leicht nachzubauen. Ich habe den Transformator aus einem alten Kosmos XG Elektronik-Experimentierbaukasten verwendet. Aber natürlich eignen sich auch andere Tonfrequenz-Übertrager. Weiter unten sind dafür noch weitere Beispiele gezeigt. |
Bericht und Video zum Experiment
Der Schaltplan des Röhrenoszillators. Laden Sie den detaillierten Bericht herunter. Hier zeige ich, wie man den Oszillator mit Hilfe der Kirchhoffschen Regeln, Knoten- und Maschenregel, verstehen kann. Das Video zeigt das Experiment dazu.
Im zweiten Teil des Berichts lesen Sie, wie es im Oszillator zur Periodenverdopplung kommt, weshalb sie ab einem gewissen Punkt plötzlich und nur unter bestimmten Bedingungen eintritt. |
|||
|
Periodenverdopplung
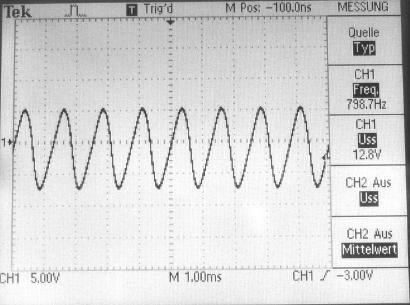
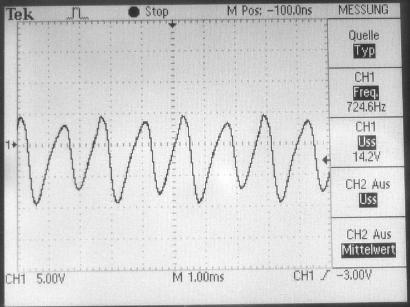
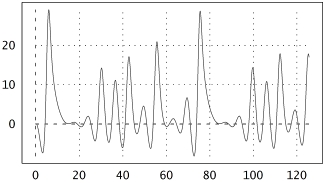
Hier ein Oszillogramm der Gitterspannung im regulären periodischen Betrieb. Die Frequenz beträgt etwa 800 Hz.
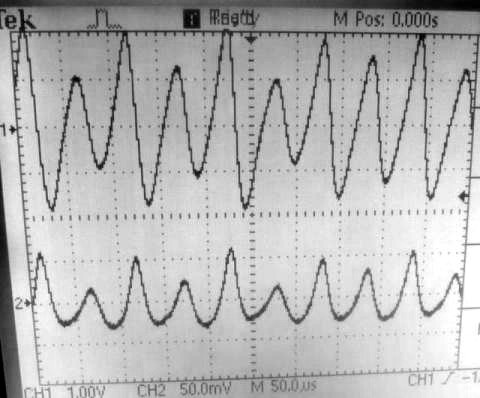
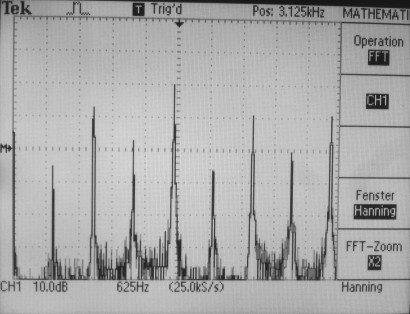
Periodenverdopplung: aufeinanderfolgende Wellenzüge verlaufen unterschiedlich. Das zeigt sich auch im Spektrum, das mein Digitaloszi dank seiner FFT-Funktion ebenfalls anzeigen kann. Im Spektrum des Oszillators erscheint bei halber Grundfrequenz eine weitere Spektrallinie. |
Mein Versuchsaufbau. Der große schwarze Schiebewiderstand (ein Rheostat aus einem aufgelösten Physiklabor) dient zur Feineinstellung der Verstärkung. Periodische und chaotische Schwingungen Der Oszillator schwingt oder er schwingt nicht. Das behauptet zumindest die landläufige Bastler-Erfahrung. Doch das ist nicht alles. Ein solcher Oszillator kann noch viel mehr, nämlich völlig irregulär und chaotisch werden. Dies passiert, sobald man den Verstärkungsfaktor der Röhre über eine kritische Grenze hinaus erhöht. Es deutet sich in kleinen Schritten an, nämlich durch eine Folge von Periodenverdopplungen (siehe Abb. links). Wenn man den Widerstand im Kathodenstromkreis, der aus den beiden Potentiometern besteht, langsam kleiner macht, dann scheint es am Oszilloskop, dass die einzelnen Schwingungszüge plötzlich zu tanzen anfangen. Sie liegen abwechselnd etwas höher oder tiefer. Die Periode des Oszillators hat sich verdoppelt. Dreht man das Poti noch weiter, dann folgt eine Vervierfachung und so weiter. Ab einem bestimmten Punkt werden die Schwingungen vollkommen chaotisch: jeder einzelne Wellenzug verläuft anders. Es wird unmöglich vorherzusagen, nach wievielen Perioden sich das Signal wiederholt. |
|||
|
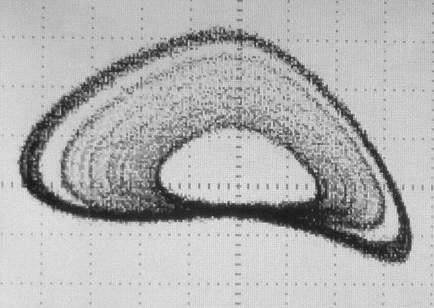
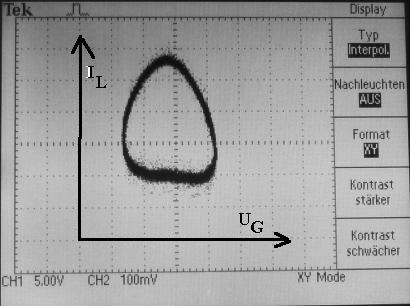
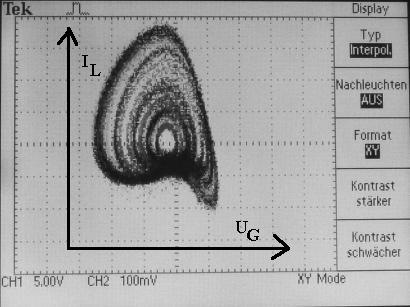
Trägt man im XY-Modus den Schwingkreisstrom IL gegen die Gitterspannung UG auf, dann zeichnet das Oszilloskop den Attraktor. Dieser beschreibt den Betriebszustand eindeutig.
Der periodische Attraktor: Zeichnet man im x/y-Modus den Schwingkreisstrom IL gegen die Gitterspannung UG auf, dann zeigt das Oszi einen leicht deformierten Kreis, der periodisch durchlaufen wird.
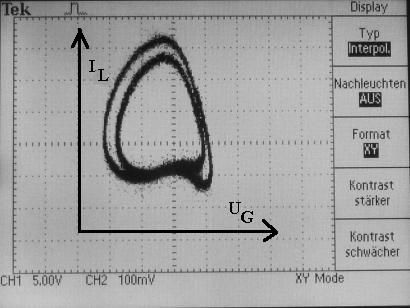
Periodenverdopplung: hier schließt der Attraktor erst nach zwei Zyklen.
Nach zwei Periodenverdopplungen zeigt der Attraktor vier Schleifen.
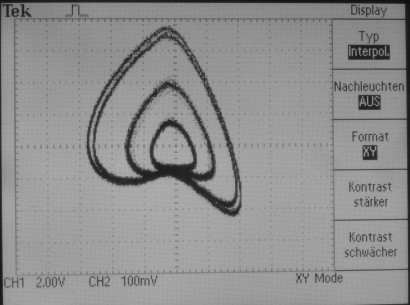
Chaotische Schwingungen: der Strom- und Spannungsverlauf IL als Funktion von UG wiederholt sich erst nach unendlich vielen Zyklen, also nie! |
Die Ursache des nichtlinearen Verhaltens Ursache ist die nichtlineare Gitterstromkennlinie der Röhre. Der Gitterstrom steigt als Funktion der Gitter-Kathodenspannung Ugk exponentiell an:
Hierbei sind:
Die Gleichung besagt, dass der Gitterstrom während der positiven Halbwelle einen Schwingung wächst. Dadurch baut sich eine zusätzliche negative Gleichspannung am Steuergitter auf. Das hat dann zur Folge, dass die Steilheit der Röhre kleiner wird und die Schwingungsamplitude des Oszillators in einer bestimmten Höhe sättigt. Dabei aber bleibt es nicht. Ab einem bestimmten Punkt ändert das gesamte rückgekoppelte System sein Verhalten: neben Vielfachen der Grundfrequenz erscheinen auch halbe, viertel, und rationale Bruchteile der Grundfrequenz, schließlich ein kontinuierliches Spektrum. Dies passiert in einem recht engen Parameterbereich. Die nichtlineare Schwingungsgleichung Mit ein wenig Praxis in den Kirchoffschen Regeln läßt sich die Differentialgleichung herleiten, die das Verhalten des Oszillators beschreibt. Das folgende gekoppelte Gleichungssystem beschreibt den Strom IL durch die Schwingkreisspule sowie die Gitterspannung UG der Röhre als Funktion der Zeit t, genaue jene Größen, die wir am Oszi aufzeichnen:
Das Fourierspektrum nach zwei Verdopplungen. Neben der Grundfrequenz (Mitte, bei f0 = 3,1 kHz) zeigt das Spektrum Linien bei halbzahligen Frequenzen (1/2 f0 = 1,55 kHz und 3/2 f0 = 4,65 kHz) sowie schwächere Linien mit viertelzahligen Frequenzen bei 1/4, 3/4, 5/4 und 7/4 f0: 775, 2.325, 3.875 und 5.425 Hz. | |||
|
Ein paar praktische Tips zu der Schaltung:
1. Wenn der Oszillator zu "pumpen" beginnt: Die Schwingungen reißen ab und setzen neu ein. Das Oszillogramm ist unruhig, doch das hat mit Chaos und Periodenvervielfachung nichts zu tun. Das Pumpen entsteht, wenn sich der Kondensator vor dem Steuergitter durch den Gitterstrom zu sehr auflädt. Die Röhre blockiert. Die Schwingungen setzen erst dann wieder ein, wenn die Ladung durch den Gittervorwiderstand wieder abgeflossen ist, bis zum nächsten Blockieren. Und so weiter. Wie wenn im Spülbecken der Abfluss verstopft ist. Abhilfe: Abfluss wieder frei machen, bzw. den Gitterwiderstand (47 kΩ) etwas verkleinern. |
2. Habe auch die Röhrentypen EF 183 und EF 184 getestet, zumal diese mit der EF 89 nahezu identische Anschlussbelegungen
haben. Diese Röhren haben aber eine höhere Steilheit als die EF 89 und benötigen einen anderen Arbeitspunkt. Ich habe den Kathodenwiderstand auf 1,5 bis 1,8 Kiloohm und den
Schirmgitterwiderstand auf 500 Kiloohm vergrößert. Der Anodenstrom ist dann etwa 0,9 mA bei 120 V Betriebsspannung. Bei diesen Spanngitterröhren entstanden z.T. jedoch intensive, sehr hochfrequente Barkhausen-Oszillationen, die die eigentlichen Tonfrequenzen überlagerten. Hier hat der Bastler noch Forschungsbedarf. Die EF 89 hat eine deutlich geringere
Tendenz zu solchen Schwingungen, auch wenn sie ab und zu da sind. Siehe Video. |
|||
|
|
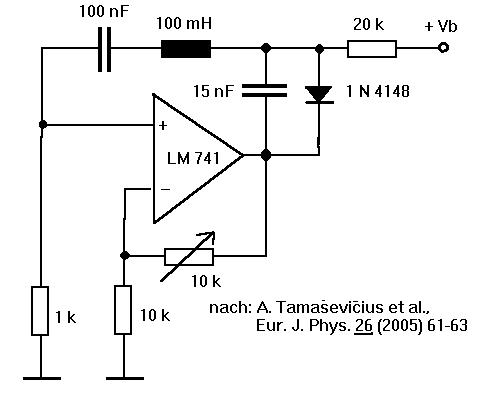
Natürlich lassen sich chaotische Phänomene auch mit Halbleiter-Oszillatoren demonstrieren. Ein schönes, leicht nachzubauendes Beispiel zeigt die Schaltung links im Bild, die eine litauische Forschergruppe vor einigen Jahren in einer Zeitschrift vorgestellt hat: zum Download. |
|||
|
10.9.16: Weitere
Experimente mit dem chaotischen Oszillator: Messung der Feigenbaum-Konstanten
|
||||
|
Nach den ersten qualitativen Versuchen zu Periodenverdopplung und Chaos wollte ich dann mehr über das Thema wissen, das weitaus tiefere Bedeutung hat, als man zunächst vermuten würde. Man hat sehr überzeugende Hinweise darauf entdeckt, dass der Übergang von regulärem Verhalten ins Chaos auch in sehr unterschiedlichen dynamischen Systemen unter vergleichbaren Vorzeichen abläuft wie in unserem Oszillator. Das Verhalten eines gekoppelten mechanischen Pendels wie etwa diesem hier. Aber auch Strömungsinstabilitäten in Wasser- und Gasturbinen, die Entwicklung von Populationen von Raub- und Beutetieren in der freien Wildbahn, neuronale Erregungsmuster im menschlichen Gehirn oder Nervengewebe, die Migräne, Herzrhytmusstörungen oder epileptische Zustände auslösen können, scheinen ähnlichen Prinzipien zu folgen. Ein wichtiges Maß hierbei ist der Abstand der einzelnen Parameterwerte, an denen eine weitere Periodenverdopplung eintritt. Man bezeichnet diese als Bifurkationen. Dieser Abstand bezieht sich auf die kritischen Werte des Kontrollparameters ε, den wir an unserem Oszillator ja leicht über die beiden Potis P1 und P2 einstellen können. Der Abstand zwischen zwei aufeinanderfolgenden Bifurkationen wird mit deren Anzahl, die der Oszillator auf seinem Weg ins Chaos durchschritten hat, immer kleiner, und zwar offenbar nach einem Exponentialgesetz. Den Faktor der Verkürzung dieses Abstandes bezeichnet man als Feigenbaum-Konstante, eine Zahl, die in verschiedensten Systemen immer gleich zu sein scheint. |
Den Oszillator habe ich diesmal mit größter Sorgfalt aufgebaut, wobei ich alle Bauelemente mechanisch mit Klebeband fixiert und für alle Betriebsspannungen einschließlich der Röhrenheizung stabilisierte Spannungen verwendet habe. Der Grund ist folgender: zur Bestimmung der Feigenbaum-Konstante muss der Oszillator mindestens 3 klar unterscheidbare Bifurkationen durchlaufen. Das erfordert eine reproduzierbare Einstellbarkeit über zwei bis drei Größenordnungen bei den Potis wie auch der Röhrenverstärkung. Störfaktoren und Spannungsschwankungen müssen deshalb so weit wie möglich ausgeschlossen werden. Der Versuchsaufbau wurde mindestens 1 Stunde vor der Messung in Betrieb genommen, um eine mögliche thermische Drift während der Messung auszuschließen. |
|||
|
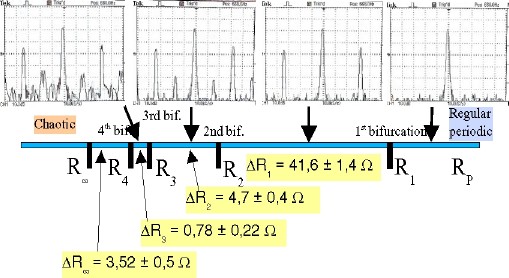
Neben dem schon bewährten Schiebewiderstand P2, der auf das Ohm genau einstellbar ist, habe ich für die Grobeinstung P1 ein 10-gängiges Präzisions-Spindelpotentiometer von 20 kΩ mit einem 100-teiligen Skalenrad verwendet. Die Widerstandsänderungen beträgt also 20 Ohm pro Teilung. Reproduzierbares Einstellen mit einer relativen Genauigkeit von etwa 10 Ohm sind dadurch möglich. Mit dieser Anordnung konnte ich Bifurkationen bis zur 3. Ordnung identifizieren. Der Abstand zwischen zwei Bifurkationen liegt hier bei unter 1 Ohm. |
Gemessene Abstände zwischen den Bifurkationen |
|||
|
Ordnung der Bifurkation |
ΔR (Ohm) |
Abstand vom Chaos-Übergang (Ohm) |
Parameterabstand Δε vom Übergang zum Chaos |
|
|
1 |
41,6 +/- 1,44 |
50,6 +/- 2,4 |
0,146 |
|
|
2 |
4,7 +/- 0,36 |
9,0 +/- 1,0 |
0,026 |
|
|
3 |
0,78 +/- 0,22 |
4,3 +/- 0,7 |
0,012 |
|
|
4 |
--- |
3,52 +/- 0,5 |
0,010 |
|
|
chaotisch |
3,52 +/- 0,5 |
--- |
0 |
|
|
Die Betriebsspannung des Oszillators habe ich auf 150 V eingestellt, die Heizspannung war 6,43 Volt. Die gesuchten Bifurkationen habe ich mittels Digitaloszi (Tektronix TDS 220) im FFT-Spektralmodus identifiziert. An den betreffenden Poti-Einstellungen sieht man, dass im Spektrum des Oszillators neue Linien bei halb-, viertel-, achtelzahligen Vielfachen der Grundfrequenz aus dem Grundrauschen zu wachsen beginnen. Die entsprechenden Potieinstellungen habe ich in die obige Tabelle eingetragen. Es handelt sich um Mittelwerte von jeweils fünf unabhängigen Messungen. |
||||
|
|
Links im Bild habe ich das Ergebnis der Messreihe noch einmal grafisch zusammengestellt, wobei ich auch jeweils die Spektren vom Oszilloskop abfotografiert habe (eingefügte Bilder oben). Die zentrale Linie stellt die Grundfrequenz des Oszillators von 660 Hz dar (bei 100 Hz pro Teilung des Oszi-Bildschirms) Mit zunehmder Zahl der Bifurkationen entstehen zusätzliche weitere Linien (von rechts nach links), bis das Spektrum im chaotischen Bereich schießlich vollkommen "dicht" ist. Die Bifurkationen von vierter Ordnung waren nicht mehr eindeutig zu identifizieren, so dass die Messreihe hier abgebrochen wurde. |
|||
|
Ergebnis Der Versuch veranschaulicht klar den Übergang von regulärer zu chaotischer Dynamik als eine Sequenz von Periodenverdopplungen, die bei stetig sich änderndem Kontrollparameter immer dichter aufeinander folgen. Wertet man nun die Verhältnisse zwischen den Abständen zweier Bifukationen aus, dann zeigen sich jedoch Abweichungen vom angenommenen Exponentialgesetz: Aus den ersten beiden Bifurkationen ergibt sich ΔR1/ΔR2 = 8,85. Dieser Wert ist zwar in der korrekten Größenordnung, doch von der Feigenbaum-Konstanten δ = 4,66920 noch um einiges entfernt. Allerdings ist dieser Wert ein Grenzwert, dem sich das Widerstandsverhältnis erst nach vielen Bifurkationen nähert. Aus der zweiten und dritten Bifurkation ergibt sich ΔR2/ΔR3 dagegen 6,03, was immerhin schon etwas besser ist. |
Literatur und weitere Informationen zum Thema: R. W. Leven, B. P. Koch, B. Pompe, Chaos in dissipativen Systemen, Akademie-Verlag Berlin 1989, ISBN 3-05-500488-4 V. Nordmeier, H.-J. Schlichting, Chaos für die Schule! Phys. Unserer Zeit, 2003, Nr. 1, S. 32 Die Originalarbeit, in der die Feigenbaum-Konstante begründet wird: Aus der Physik-am-Samstag-Website von S. Lück mit vielen Experimenten: Die Erforschung des Chaos. |
|||
| 22.9.16: Wir simulieren den chaotischen Oszillator nummerisch | ||||
|
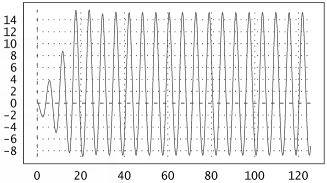
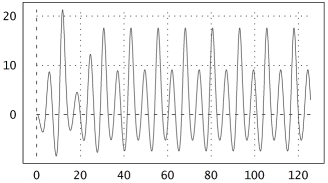
Eine Differentialgleichungen für den Oszillator ist ja ganz nett. Da sie zu kompliziert ist, dass man sie mit den üblichen Methoden von Hand lösen kann, habe ich es mit Simulation versucht. Der PC erledigt dann die Arbeit auf nummerischem Wege. Dazu empfiehlt es sich, die Gleichungen in ein System von Differentialgleichungen erster Ordnung umzuformen. Das Resultat ist rechts gezeigt. Ich habe dazu dimensionslose Variablen x, y und z. Die Variable x ist bis auf Vorfaktoren der Schwingkreisstrom IL, y die Zeitableitung des Stroms und z die Spannung UG am Steuergitter. Zum Rechnen habe ich die Euler Math Toolbox verwendet, die man sich hier kostenlos herunterladen und installieren kann. Ich habe dafür ein entsprechendes Skript geschrieben (Box rechts unten), das die Gleichung mit dem Runge-Kutta-Verfahren über einen Zeitraum von 20 Schwingungsperioden integriert: τ geht von 0 bis 125.6 (das sind 40 π). Ferner ist γ = 1.3 V-1 x 300 mV = 0.4. Der Kernbestandteil ist der dreikomponentige Vektor [x,y,z]. Seine Zeitableitung ist laut Differentialgleichung eine Funktion des Vektors: [dx/dt,dy/dt,dz/dt] = osc[t,x,y,z] Die Euler-Funktion "runge" integriert nun in kleinen Zeitschritten von 0.002 Zeiteinheiten den Lösungsvektor, beginnend mit den Anfangsbedingungen x = 0.1, y = 0, z = 0 bei τ = 0. Nicht sehr kompliziert! Die Spannung am Steuergitter habe ich unten für verschiedene Werte von ε geplottet. Euler-Skripte sind (sofern man den entsprechenden Modus aktiviert) mit der Mathematik-Software MATLAB weitgehend kompatibel. |
|
|||
|
.. Chaotischer Oszillator |
||||
|
|
|
|||
|
|
|
|||
|
Schlussfolgerung: Ich habe natürlich auch versucht, die Bifurkationspunkte aufzusuchen und die Feigenbaum-Konstante aus der Simulation zu bestimmen. Die Werte, die ich für die verschiedenen Konstanten angenommen habe, sind im oben gezeigten Euler-Skript eingetragen. An Hand der ε-Werte der ersten drei Bifurkationen habe ich damit einen Schätzwert δ1 = 5,3 für die Feigenbaum-Konstante erhalten. Die Ergebnisse zeigen, dass unsere Analyse des Oszillators zumindest qualitativ korrekt ist und die wesentlichen Merkmale des Übergangs vom regulären in den chaotischen Betriebszustand erfasst. |
||||
|
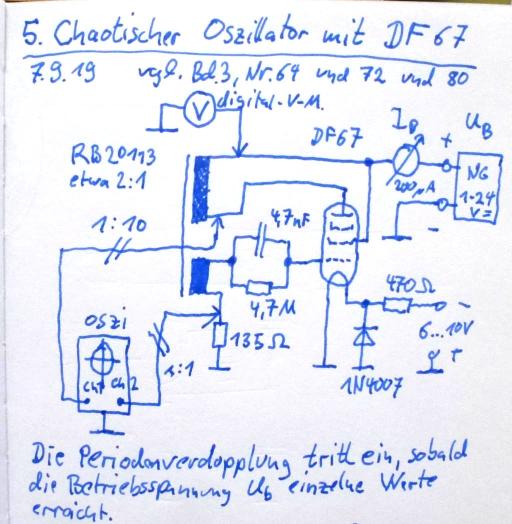
18.9.2019: Weitere Schaltungen - Chaotischer Oszillator mit Batterieröhre DF67 |
||||
|
Lassen sich die Periodenverdopplungen und die chaotischen Schwingungen auch bei niedriger Betriebsspannung und mit Batterieröhren demonstrieren, wurde ich neulich gefragt? Im Prinzip geht das selbstverständlich. Dann habe ich mich aber doch an den Basteltisch gesetzt, weil ich wusste, dass ich seit Jahren eine Miniatur-Pentode DF67 in der Bastelkiste hatte.
DIe DF 67 ist eine winzige Stiftröhre, die über ihre dünnen Drahtbeinchen angeschlossen wird. Sie wurde für den Mikrofonverstärker in Hörgeräten konzipiert, und der maximal zulässige Kathodenstrom. liegt bei nur 75 µA. Bisher hatte ich dafür noch keine rechte Verwendung gefunden. Dafür sind Heizspannung (0,625 V) und Heizstrom (13 mA) äußerst bescheiden. Ein Hörgerät muss mit der Batterie schließlich viele Stunden lang auskommen. Die Steilheit der DF 67 wird im Datenblatt mit 0,1 mA/V angegeben. Wenig im Vergleich zur EF 89, die 4 mA/V bringt. Ob das reicht ? Man braucht ja für die Periodenverdopplung eine gewisse Mindestverstärkung. Um es kurz zu machen: ich war von dem kleinen Röhrchen begeistert! Sofort hatte ich Schwingungen, und, kaum dass die Betriebsspannung 15 Volt erreichte, gab es die erste Periodenverdopplung. Die Oszillatorschaltung ist wirklich sehr sehr simpel. |
||||
Hier die Schaltung und der Aufbau auf dem Steckbrett.
Zur leichten Montage und zur Entlastung der filigranen Anschlussdrähte habe ich die Röhre sowie eine entsprechende fünfpolige Stiftleiste im 2,54-mm-Rastermaß auf eine Lochrasterplatte gelötet. Um die Heizspannung von 0,625 V stets genau einstellen zu können, habe ich parallel zum Heizfaden eine Siliziumdiode (1N4007) eingelötet. Diese besitzt in Durchgangsrichtung eine stabile Schwellenspannung von 0,6 bis 0,7 V: genau richtig für den Heizfaden der Röhre. Zum Heizen klemme ich den mit der Diode gesicherten Heizfaden über einen Widerstand von 470 Ohm an eine Batterie oder an ein Gleichspannungs-Netzteil von 6 bis 10 Volt.
Der kleine Rückkopplungstrafo mit der aufgedruckten Nummer RB-20113 ist ein Tonfrequenzübertrager aus einem japanischen Transistorradio der 1970er Jahre, dessen Fragmente ich ebenfalls in meiner Bastelkiste archiviert hatte. Toshiba oder Sanyo. Solche Teile, auch die Germaniumtransistoren und Ferritantennen, sollte man niemals wegwerfen, denn sie werden heute kaum mehr hergestellt und sind für den Elektronikbastler Gold wert. Damals ein Pfennigsartikel aus Massenproduktion, heute nur als horrend teure Spezialanfertigung zu bekommen. Das Windungsverhältnis des kaum 2 cm großen Trafos zwischen Anoden- und Gitterspule ist 2:1. Zur Schaltung selbst muss ich, glaube ich, nichts mehr sagen. Wenn man die Heizspannung anlegt und die Betriebsspannung (aus dem Netzgerät) langsam von Null hochdreht, dann setzen bei mir die Schwingungen bei ungefähr 10 Volt ein. Die Frequenz liegt bei 15 kHz. Im Bereich zwischen 14 und 15 Volt zeigen sich dann die gewünschten chaotischen Effekte. Dreht man die Spannung noch höher, dann arbeitet der Oszillator als einfacher Sperrschwinger, ohne chaostechnisch interessante Effekte. |
|
|||
|
26.1.2020: Chaotischer Oszillator: mit dem Transistor klappt es auch |
||||
|
Es wäre natürlich unlogisch gewesen zu vermuten, dass ich diese Frage nicht irgendwann untersuchen würde. Die klare Antwort: es geht! Doch das war ein langes Stück Arbeit, länger als erwartet. Zuerst hatte ich versucht, mit einem Silizium-Transistor einen chaotisch arbeitenden Meißner-Oszillator aufzubauen. Dabei kamen absolut funktionstüchtige Oszillatoren heraus. Das hatte ich nicht anders erwartet. Solche für sinusförmige, harmonische Schwingungen, andere arbeiteten hervorragend als Sperrschwinger und erzeugten am Oszilloskop scharfe Impulsspitzen. Doch eine Periodenverdopplung? Ein chaotischer Übergang? Fehlanzeige. Ich biss auf Granit, besser gesagt, auf Silizium, das noch viel härter ist. Genau das aber war die entscheidende Erkenntnis: Die Emitter-Basis-Diode eines Silizium-Transistors hat wie die Gitter-Basis-Kennline einer Röhre einen nichtlinearen Bereich. Das ist für das chaotische Verhalten, wie wir wissen, essentiell. Doch ist dieser Bereich bei Silizium-Elementen sehr viel schmaler als bei Röhren. Das Problem liegt nicht bei den Transistoren an sich, sondern darin, dass ich die Betriebsbedingungen mit meinen einfachen Mitteln nicht genau genug einstellen kann. Die Lösung des Problems waren Transistoren mit Germanium als Halbleiter, wie sie ab 1960 hergestellt wurden. Die Basis-Emitter-Kennlinie hat zwar auch hier schon einen deutlich kantigeren Knick als bei Röhren, doch sehen die Strom-Spannungs-Kennlinien noch immer deutlich runder aus als bei Silizium. Vielleicht liegt es auch einfach an den hohen Exemplarstreuungen innerhalb der frühen Transistor-Typenreihen, wofür Germanium-Halbleiter ja berüchtigt waren. 
Von links nach rechts: Germanium-Transistoren der 1960- und 70er Jahren von den damals führenden Marken der Elektronikindustrie: 2SB54 und 56 sind NF-Typen von Toshiba aus der ersten Generation von Transistoren, die am Ende der Röhrenära reichlich in den sprichwörtlichen Billigradios und -kasettenrekordern aus Japan verwendet wurden. 2SB172, 173 und 175 stammen aus den Werken von Matushita und dientem dem gleichen Zweck. Mitte: Komplementäre Ge-Transistoren AC187 und 188 von Siemens für die transformatorlose Verstärkerendstufe. Daneben einTF 78/30 von Telefunken. Rechts: Ein OX7004 der Nürnberger Firma MIRA Elektronik, die ihre Radios mit Transistoren einer eigenen Serie ausstattete. Hergestellt wurden diese Transistoren bei TeKaDe, damals ebenfalls in Nürnberg ansässig. Mehr dazu können Sie hier lesen . Im selben Bild daneben ein Miniatur-Ausgangsübertrager aus damaliger japanischer Produktion mit kaum mehr als 1 cm Kantenlänge. |
||||
|
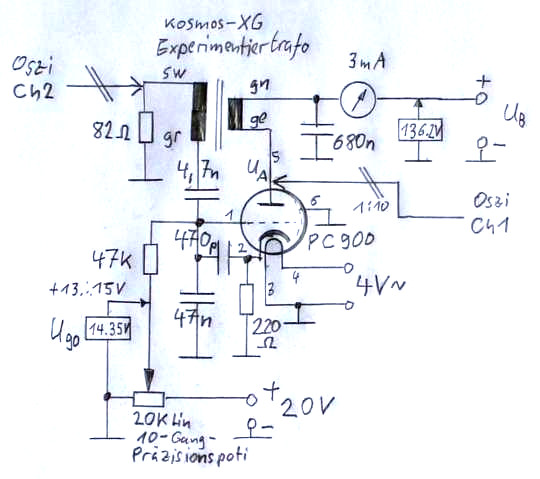
Hier die Schaltung und der Aufbau auf dem Steckbrett.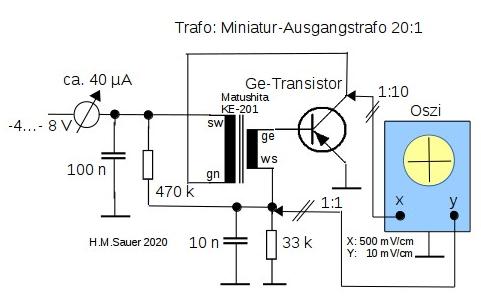 
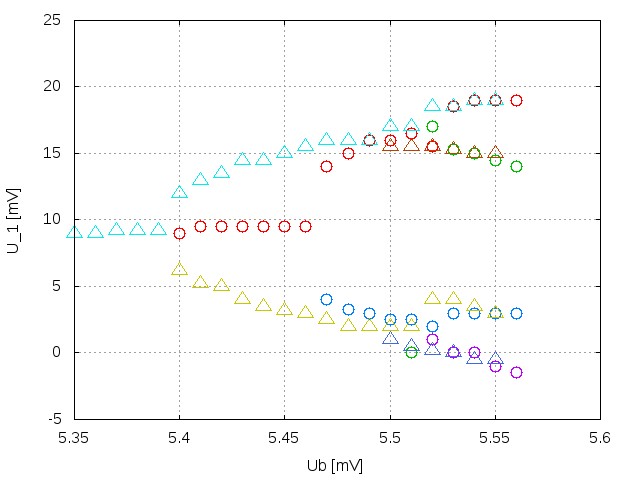
Der Oszillator arbeitet nach dem Meißner-Prinzip und besitzt auf den ersten Blick keine Besonderheit. Jedoch habe ich als Transformator einen solchen mit hohem Übersetzungsverhältnis gewählt. Die Spannung aus dem Kollektorkreis wird im Verhältnis 20:1 für den Basiskreis herabgesetzt. Entsprechend höher ist auch der Strom, der für die Emitter-Basis-Diode zur Verfügung steht. Beim Röhrenoszillator war dieser Aspekt nebensächlich. Beim Bipolartransistor ist der Eingangswiderstand viel kleiner, und damit ist der Strom wichtig. Zur Auswahl eines geeigneten Transistors kann ich nur wenig sagen. Ich selbst erzielte mit einem 2SB56 von Toshiba und mit einem OX 7004 von Mira die besten Resultate, aber die sind aus dem ganz zufälligen Inhalt meiner Bastelkiste. Äquivalente Typen wie AC122 oder 126 sind gewiss aussichtsreiche Kandidaten. Aber es funktionierte nicht mit allen Ge-Transistoren, auch nicht mit einem uralten OC75 von Telefunken, der noch im schwarzlackierten röhrenähnlichen Glaskolben daherkam. Er verhielt sich in diesem Punkt als hätte er das Silizium höchstpersönlich erfunden. Die Frequenz des Oszillators hängt natürlich in erster Linie von der Induktivität der Trafowicklung ab und lag bei 15 kHz. Die verschiedenen Schwingungsarten und Periodenverdopplungen werden durch Veränderung der Betriebsspannung eingestellt. Das muss man ausprobieren, wobei ein sehr fein einstellbarer Spannungsregler unbedingt zu empfehlen ist. Bei mir ereignete sich der Übergang zum chaotischen Verhalten im Bereich zwischen −5,40 und −5,57 V. Es lohnt also, die Betriebsspannung im betreffenden Bereich mit einem Digitalmultimeter auf 10 mV genau zu bestimmen, um alles genau und reproduzierbar nachverfolgen zu können. Dafür konnte ich in den Versuchen mit dem 2SB56 gleich zwei aufeinanderfolgenden Bifurkationen beobachten und sauber untersuchen. Bei Röhren, siehe oben, ging das mit einer Sequenz von drei Bifurkationen.
Dieses Diagramm habe ich erzeugt, indem ich mir den Attraktor der Oszillatorschwingungen am Oszi im X-Y-Modus angesehen habe. Diesen habe ich in der Bildmitte zentriert und dann die Spannungswerte an den Schnittpunkten mit der positiven Y-Achse des Koordinatenkreuzes auf dem Bildschirm notiert. Dann habe ich die Betriebsspannung von −5.35 Volt (da waren der Attraktor ein einfacher Ring) in 10-mV-Schritten bis knapp −5.6 V (da war es chaotisch) erhöht und die Werte immer wieder notiert (Kreissymbole). Je nach Anzahl der Bifurkationen gibt es dann 2 oder 4 Schnittpunkte. Dann habe ich das gleiche in umgekehrte Richtung wiederholt, bis die Schwingungen wieder regulär waren (Dreieckssymbole). Man sieht übrigens, das die beiden Messreihen nicht genau aufeinander liegen. Es gibt hier also eine gewisse Hysterese der Schwingungsbereiche. |
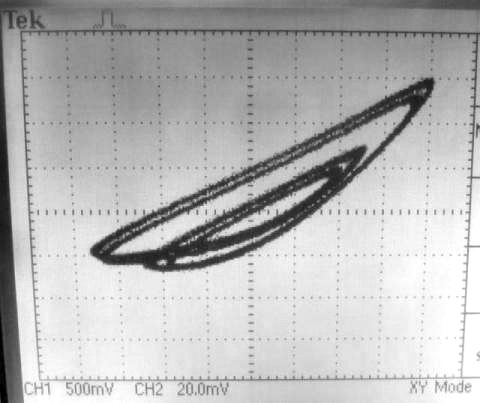
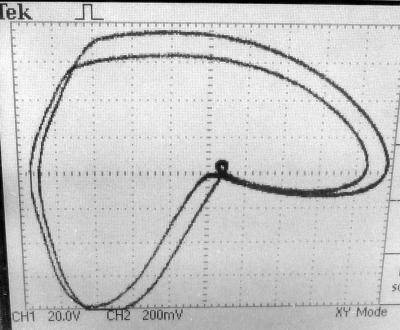
Im X-Y-Modus des Oszilloskops ergibt sich diese Figur. Es schaut schon anders aus als beim Röhrenoszillator, aber er Vervielfachung der Zyklen ist auch hier unverkennbar.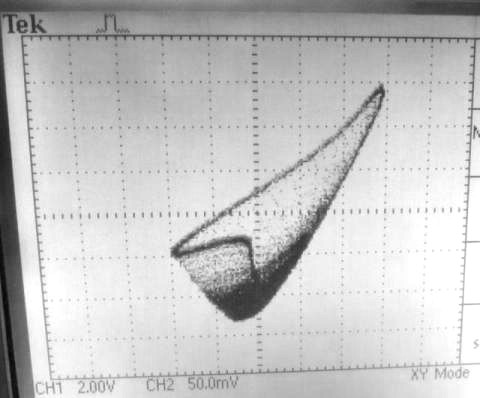 
Im X-Y-Modus erzeugt der chaotische Zustand sogar ästhetische Formen. Zurück zum Anfang |
|||
|
Aufbau und Schaltung des Oszillators
Eine ultrasteile Triode PC900 aus einem TV-Tuner produziert besonders gut reproduzierbare Periodenverdopplungen und chaotische Schwingungen. Mit PC86 und 88 funktioniert es ebenfalls.
Die Schaltung unterscheidet sich praktisch nicht von derjenigen ganz oben. Der Arbeitspunkt wird mittels eines Präzisionspotis auf 10 mV genau über die positive Gittervorspannung Ug0 eingestellt. Die Betriebsspanung von hier 136.2 V wurde mittels Digitalmultimeter auf das zehntel Volt genau konstant gehalten. Um Klystron-Oszillationen mit Frequenzen im UKW-Bereich zu unterdrücken, die bei solchen sehr steilen Trioden gern entstehen, musste ich über ganz kurze Anschlussdrähte einen HF-tauglichen 470-pF-Kondensator direkt zwischen Gitter und Kathode schalten.
Der Attraktor nach der ersten Periodenverdopplung zeigt den Strom im Gitterkreis als Funktion der Anodenspannung UA. |
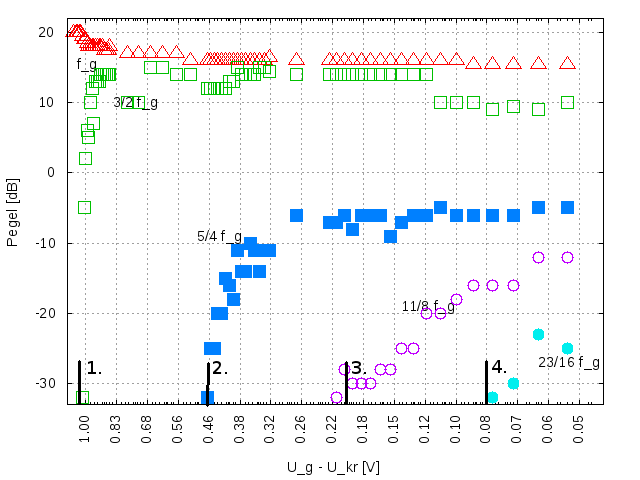
Die Abfolge der Periodenverdopplungen Mit dieser Schaltung konnte ich eine Folge von vier Periodenverdopplungen herbeiführen. Rekord! Der chaotische Übergang lag als Funktion der Gittervorspannung Ug0 bei Ukr = 13.48 V. Die Verdopplungen traten bei Spannungen auf, die um 1.01, 0.46, 0.20 und 0.06 V darüber lagen.
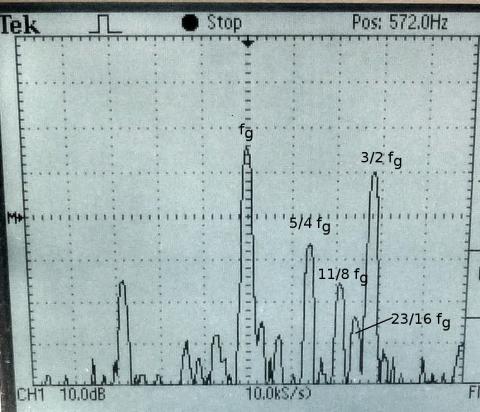
Dieses Diagramm zeigt die Amplitude der Schwingungskomponeten mit halb,- viertel-, achtel- und sechzehntelzahligen Vielfachen der Grundfrequenz fg = 572 Hz als Funktion der positiven Gittervorspannung (abzüglich Ukr) auf der logarithmische Skala dar. Die roten Messpunkt zeigen die Amplitude der Grundschwingung, die bei etwa 17 dB (mit 0 dB = 1 V) liegt. Grün ist die Amplitude der Schwingung mit der Frequenz 3/2 fg, die bei 1.01 V über der Messschwelle von -30 dB tritt. Die dunkelblauen Quadrate, violetten Kreise und türkisblauen Scheiben entsprechen den Frequenzanteilen von 5/4, 11/8 bzw. 23/16 der Grundfrequenz. Sie besitzen unter den neu hinzukommenden Frequenzen die jeweils höchsten Amplituden und befanden sich im Spektrum immer direkt unterhalb der Frequenzkomponente 3/2 fg aus der ersten Periodenverdopplung. Das ist etwas anders als in der Pentodenschaltung, wo eher die Frequenzkomponenten unterhalb der Grundfrequenz dominant sind.
Hier ein Schnappschuss vom Oszilloskop, der das Spektrum im FFT-Modus zeigt. Mittenfrequenz ist 572 Hz, die Teilung der Frequenzachse ist 100 Hz/cm. Die vertikale Achse hat eine Teilung von 10 dB/cm. Ein paar technische Details: ich habe die Flattop-Fensterfunktion des FFT-Moduls verwendet. Zur besseren Stabilität des Oszillogramms habe ich "Aquire" auf 16-fach-Sampling eingestellt. |
|||
|
Zurück zum Anfang Hans Martin Sauer 2016-2021 |
||||
Wege ins Chaos, und wieder heraus !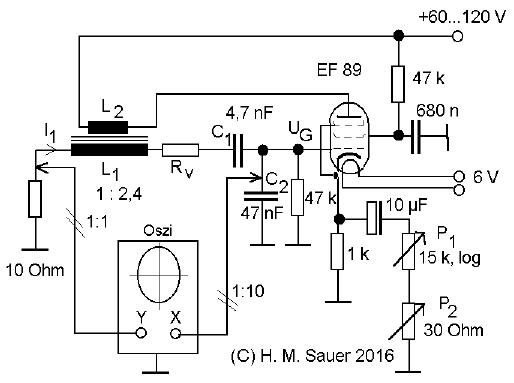 
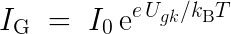
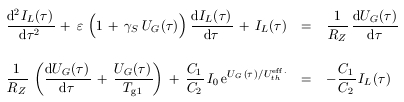
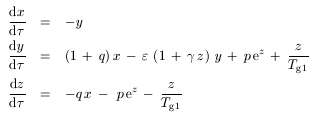
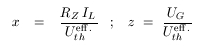
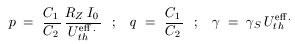
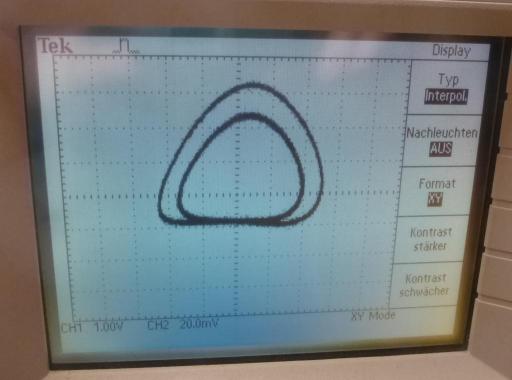Dieser Attraktor (Gitterstrom vs. Anodenspannung im XY-Modus des Oszis) zeigt die erste Periodenverdopplung, bei 14,74 Volt. Bei 14,99 Volt tratt die Vervierfachung auf, bei 15,14 V die Verachtfachung. 
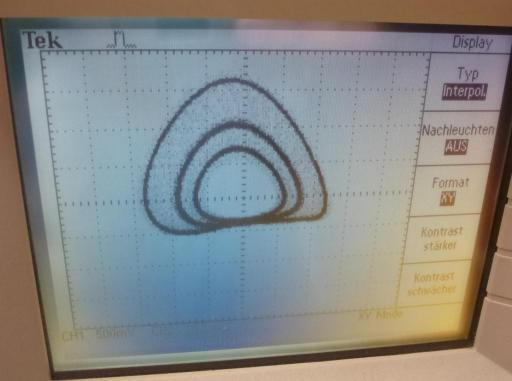Auch eine Verdreifachung konnte ich erreichen. Wie geht das denn? Im Spannungsbereich, wo die Schwingungen schon chaotisch sind, fand ich eine "Insel der Regularität" mit diesem interessanten Phänomen. Die war aber sehr schmal, und es bedurfte echtes Fingerspitzengefühl am Spannungsregler. 
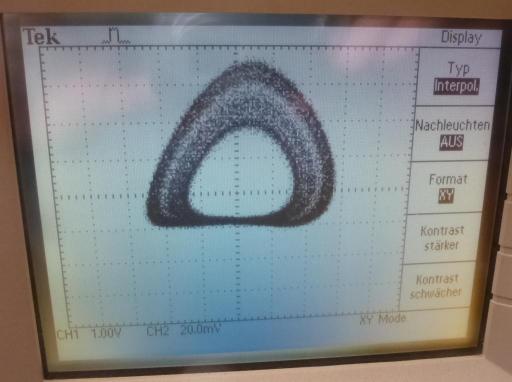Und zum Schluss ein chaotischer Attraktor.
