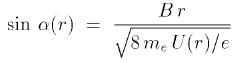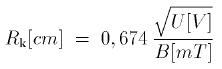Wenn man im Vakuum einen Elektronenstrahl durch ein Magnetfeld schickt, dann wird er aus der geraden Richtung abgelenkt. Die Rechte-Hand-Regel (Wer erinnert sich an den Physikunterricht?) besagt: in einem magnetischen Feld B erfährt eine bewegte elektrische Ladung e eine Lorentzkraft

F_L = e B x v,

die senkrecht zu ihrer Bewegungsrichtung v wirkt. Das zeigt das zweite Bild rechts. Dadurch müsste man sie doch auf eine Kreisbahn lenken können, nicht wahr ? Der Bahnradius r ist dann gerade so groß, dass die nach außen zeigende Zentrifugalkraft die nach innen gerichtete Lorentzkraft kompensiert:

F_z = m_e v² / r e_r

m_e ist die Masse des Elektrons, e_r der radial nach außen gerichtete Einheitsvektor. Wenn die Elektronen im Kreis fliegen statt auf geradem Wege zur Anode, dann sollte sich das am Anodenstrom bemerkbar machen, so meine erste Überlegung. Jedenfalls wenn das Magnetfeld stark genug ist. Also habe ich eine Pentode vom Typ EL84 genommen und in den Experimentiersockel gesteckt. Diesen habe ich dann an mein Labornetzgerät angeschlossen: Heizung an, Kathode an Minus, Anode und Schirmgitter an Plus, dann noch eine negative Spannung von -10 Volt ans Steuergitter. Bei 200 Volt Andenspannung konnte ich etwa 20 mA Anodenstrom messen. Soweit ist das in Ordnung. Jetzt das Magnetfeld, das die Elektronen umlenken soll: wenn ich einen starken Magneten, einen Neodym-Eisen-Bor-Supermagneten, an den Glaskolben der Röhre halte, dann, ja müsste dann nicht der Strom abnehmen? Doch es passiert nichts! Der Zeiger des Milliamperemeters rührt sich keinen Millimeter. So einfach ist die Sache dann doch nicht.

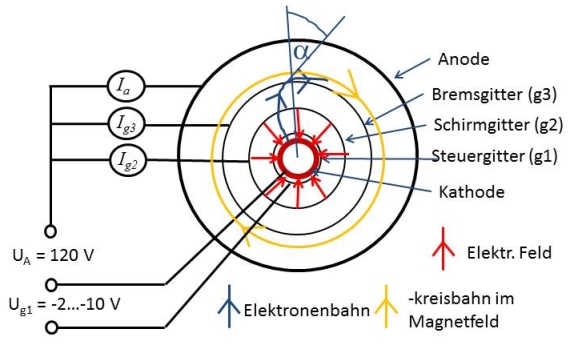
Wird so die Bahn der Elek­tronen (blau) in der Röhre aus­sehen, wenn ein Magnet­feld anliegt, das senk­recht zur Bild­ebene zeigt? Die Zeichnung zeigt den Aufbau einer Radio­pentode und den "Flug­plan" der Elek­tronen im Magnet­feld. Sie nehmen im elek­tri­schen Feld zwischen Kathode und Schirm­gitter Ge­schwin­dig­keit in radiale Richtung auf, geraten aber wegen der magne­tischen Lorentz­kraft auf eine Kreis­bahn, die zwischen Schirm­gitter und Anode um das Zentrum, die Kathode, führt. Das wollen wir demon­strieren.

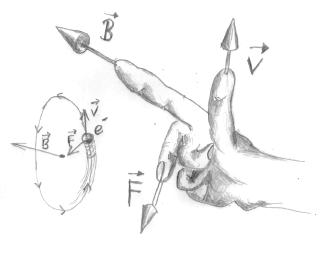
Die Rechte-Hand-Regel: der Daumen zeigt die Bewe­gungs­rich­tung an, der Zeige­finger das Magnet­feld, und der Mittel­finger die Ablenk­kraft zum Mittel­punkt des Kreises, den die Elek­trone­nbahn beschreibt. Aber Achtung: Elek­tronen sind negativ geladen. Dadurch kehrt sich die Kraft­richtung genau um!

Hier eine EF 184 im Versuchs­aufbau. Rechts die Magnet­spule, die das magne­tische Feld erzeu­gen soll.

Die anfangs verwen­dete EL84 musste ich durch eine EF 89, EF 183 oder EF 184 ersetzen. In der EL 84 ist das Brems­gitter intern mit der Kathode verbun­den. Bei einer EF 89 und den anderen Pen­toden ist das Brems­gitter dagegen über einen eigenen Ans­chluss nach außen geführt. Die Anschlüs­se von Schirm­gitter, Brems­gitter und Anode habe ich über ein Milli­ampere­meter (bezie­hungs­weise jeweils über einen kleinen Wider­stand, an dem ich per Oszil­loskop den Spannungs­abfall messe) gemein­sam an +120 Volt aus dem Netz­gerät geklemmt.

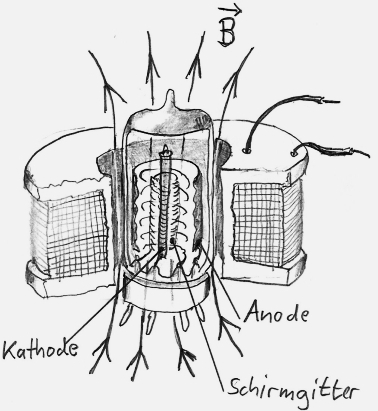
Der verbesserte Versuchs­aufbau. Zunächst habe ich über die Röhre eine Zylinder­spule gestülpt, deren Feld zur Achse des Röhren­systems paral­lel liegt. Schirm­gitter, Brems­gitter und Anode liegen ferner auf dem gleichen Poten­tial. Zwischen dem Schirm­gitter und der Anode gibt es also kein elek­trisches Feld. Hier wirkt auf die Elek­tronen keine elektro­sta­tische Kraft, sondern nur die magne­tische Lorentz­kraft.

Die Überlegung dabei ist, dass die Elek­tronen im Zwischen­raum zwischen Schirm­gitter und Anode durch das Magnet­feld wie in einer Zirkus­arena auf eine Kreis­bahn gelenkt werden. Hier können sie viele Runden drehen und lange verweilen, bevor sie vom nächst­lie­genden Gitter oder von der Anode absor­biert werden. Das hängt vom Radius ihrer Bahn­kurve ab, der sich durch die Stärke des Magnet­feldes ja beein­flussen lässt. Wenn der Radius ihrer Bahn demje­nigen einer Elek­trode ent­spricht, dann müsste sich der Strom, der durch diese Elek­trode fließt, erhöhen.

Das Magnetfeld

Woher aber weiß ich, wie stark das Magnet­feld meiner Spule ist, wenn ich da einen bestimm­ten Strom hin­durch schicke, sagen wir 1 Ampere? Ganz ein­fach, das berechne ich mit dem L-Culator! Aus den Maßen der Wick­lung und der Windungs­zahl kann ich mit diesem Tool die Feld­stärke im Zentrum der Spule bestim­men. Die hier verwen­dete Zylinder­spule hat 530 Win­dungen aus 0,6 mm starkem Kupfer­lack­draht. Die Wick­lung hat einen Innen­durch­messer von 2,5 cm, einen Außen­durch­messer von 5 cm und eine Länge von 2,7 cm. Aus diesen Anga­ben berechnet der L-Culator eine Feld­stärke von 15 mT bei 1 A Spulen­strom. Kurz­zeitig hält die Spule sogar 4 A aus, das ergibt dann maxial 60 mT. Das genügt für dieses Experi­ment vollauf. Der Strom hierzu kommt aus einem regel­baren Labor­netz­gerät, das genügend Ampere liefern kann. Bei 4 Ampere verpul­vert die Spule etwa 75 Watt Leistung, sagt der L-Culator.

Die Spule sitzt auf der Röhre. Ich habe einfach eine passende Klammer aus Alublech zurechtgebogen, um das Zentrum der Spule über dem Röhrensystem zu positionieren. Jetzt kann der Versuch losgehen.

Der Versuchsaufbau. Zusätzlich habe ich ein Oszilloskop angeschlossen, das hier im Bild nicht zu sehen ist.

Links im Bild die Gesamtübersicht über den Versuchsaufbau: Hinten links das Netzgerät für die Anoden- und Gitterspannung, dieses hier. Rechts daneben das Labornetzgerät für den Magneten, mit eingebautem Amperemeter. Es ist aber nützlich noch ein genaueres Amperemeter in die Spulenleitung zu schalten. Vorne ein Vielfachinstrument, dass den Strom durch das betreffende Gitter g₂, g₃ oder der Anode mißt. Die Spule mit der Röhre darunter in der Bildmitte. Ich habe ihr wegen der hohen Verlustleistung einen kleinen Ventilator gegönnt, der während der Messung für etwas Kühlung sorgt.

Wenn man nun den Spulenstrom langsam Stück für Stück hochdreht, dann kann man am Milliamperemeter die Ströme als Funktion des Spulenstroms und damit des Magnetfelds ablesen. Ich habe anfangs alles noch von Hand in eine Tabelle eingetragen. Das ist etwas mühsam. Praktischer ist es natürlich, wenn man das alles mit einem Digitaloszilloskop erledigt (so habe ich es am Ende auch gemacht). Man fährt mit dem Magnetfeld eine "Rampe" und zeichnet auf der x-Achse den Erregerstrom, auf der y-Achse den Strom durch die jeweilige Elektrode auf. Das Ergebnis ist aber das Gleiche.

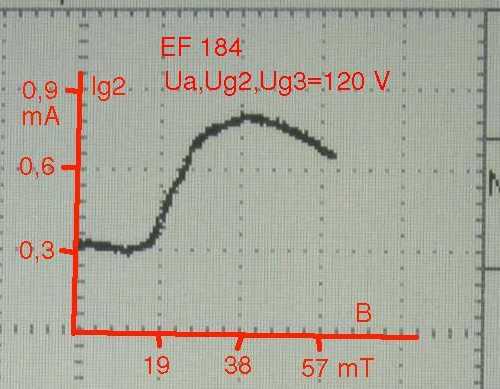
Nun zu den Ergebnissen:

Das Bild rechts zeigt den Strom I₂ durch das Schirmgitter einer EF 184 als Funktion des Magnetfeldes B, angegeben in Millitesla. Sorry für die etwas "krummen" Zahlenwerte an der x-Achse, aber ich habe den Proportionalitätsfaktor zwischen Magnetfeld und Spulenstrom (nur den mißt das Oszi) erst nachträglich berechnet.

Ohne Magnetfeld fließt hier ein Strom von 0,3 mA, der zunächst auch vom Magnetfeld unabhängig ist. Erst ab etwa 16-17 mT steigt der Schirmgitterstrom an und erreicht bei 40 mT ein Maximum.

Was passiert hier? Nun, unterhalb von 16 mT ist das Feld zu schwach, um die Elektronen überhaupt von ihrem Weg zum Bremsgitter oder zur Anode abzulenken. Dann aber, bei noch stärkerem Feld, werden immer mehr Elektronen zum Schirmgitter zurückgelenkt. Der Strom steigt. Bei Feldern oberhalb von 40 mT wird die Ablenkung dann so stark, das die Elektronen von der Kathode nicht einmal mehr bis zum Schirmgitter gelangen können.

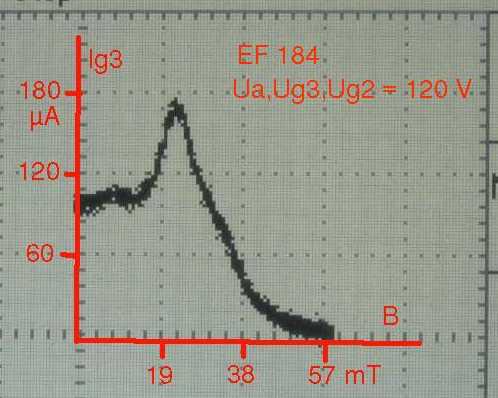
Sehen wir uns nun das Bremsgitter der EF 184 an. Zunächst fällt auf, dass der Bremsgitterstrom sehr viel kleiner ist als der Schirmgitterstrom, obwohl beide Gitter doch auf dem gleichen Potential liegen. Das liegt daran, dass das Bremsgitter viel weitere Maschen hat (tatsächlich ist es bei der EF 184 bloß ein Blech mit weiten Öffnungen), und dass die Elektronen die Gitterdrähte nicht ganz so leicht finden.

Man erkennt hier jedoch ein scharfes Maximum des Gitterstroms bei etwa 22 mT. Die Elektronen sind bei dieser Feldstärke offenbar auf einer Kreisbahn um die zentrale Kathode der Röhre, und der Radius der Kreisbahn entspricht dem Radius des Bremsgitters. Die Wahrscheinlichkeit, auf das Bremsgitter zu treffen, ist dann also besonders hoch. Ändert man die Feldstärke, dann wird die Kreisbahn enger oder weiter, jedenfalls führt sie dann am Bremsgitter vorbei. Der Strom I_g3 nimmt in jedem Falle stark ab.

Der Bremsgitterstrom verschwindet schließlich oberhalb von ca. 50 mT. Kein Elektron gelangt nunmehr so weit nach außen.

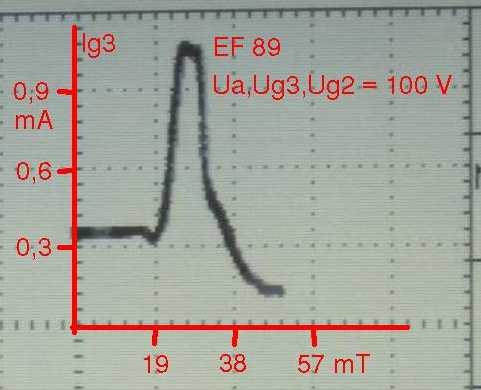
Rechts im Bild das Ergebnis des gleichen Versuchs mit einer EF 89. Das ist eine "gewöhnliche" Pentode mit einem ringsum gewendelten Bremsgitter. Im Unterschied dazu hat die EF 184 als sogenannte "Strahlbündeltetrode" als Bremsgitter nur zwei schmale Blechstreifen vor der Anode, die wohl von den Elektronen selten angeflogen werden. Bei der EF 89 beobachtet man daher ein viel ausgeprägteres Maximum des Bremsgitterstroms. Bei Feldstärken um 25-28 mT ist I_g3 auf mehr als das Dreifache gegenüber der EF 184 angewachsen.

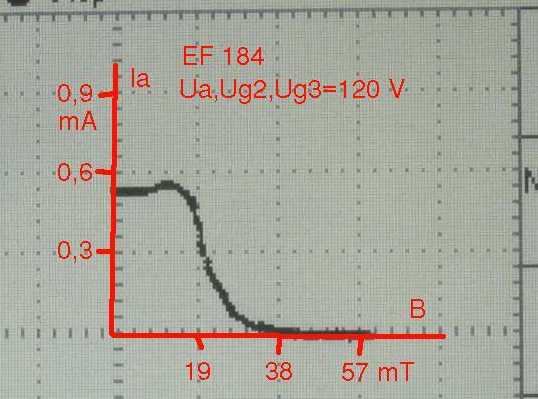
Zuletzt der Strom durch die Äußerste der Röhrenelektroden, die Anode. Der Anodenstrom verschwindet oberhalb von 30 mT praktisch vollständig. Das war zu erwarten. Die Elektronen fliegen auf engen Kreisbahnen, die sie zu Schirm- oder Bremsgitter führen.

Ein wenig Theorie zum Schluss

Der Ablenkwinkel α, um den die Elektronenbahn von der radialen Bewegungsrichtung zwischen der Kathode und der Anode der Röhre abweicht, beträgt (hierzu muß man die Lorentzkraft berechnen, die auf das Elektron wirkt):

m_e = 9,109 10^-31 kg ist hierbei die Elektromenmasse, e = 1,602 10^-19 C die Elementarladung, r der Abstand von der Kathode (in m), U(r) das Potential an diesem Punkt (in Volt), und B die magnetische Feldstärke (in Tesla). Die Kreisbahn ist erreicht, wenn α gleich 90° ist. Der Sinus ist dann gleich 1. Für den Bahnradius R_k kann man nun folgende Formel angeben, wobei die genannten Naturkonstanten in dem nummerischen Vorfaktor stecken:

Bei der EF 184 haben wir im Versuch eine Spannung von 120 V an die Anode und die beiden äußeren Gitter angelegt. Das Maximum des Bremsgitterstroms beobachteten wir bei B = 22 mT. Das bedeutet, dass der Radius der Kreisbahn hier mit dem Radius des Bremsgitter(blech)s identisch sein sollte. Die Formel ergibt einen Radius von 3,4 mm, was für diese Bauform der Röhre durchaus realistisch erscheint.

Zum Anfang der Seite

Hans Martin Sauer 2016-2020